DE CERO A ÁLEF: MATEMÁTICAS Y JUDAÍSMO, CON AMELIA MUÑOZ GARCÍA - Paul Joseph Cohen (1934-2007) fue un matemático estadounidense judío, que destacó por su contribución fundamental en la lógica matemática al demostrar que la hipótesis del continuo y el axioma de elección son ambos independientes de los axiomas de Zermelo-Fraenkel, es decir, el primero de los Problemas de Hilbert. Por ello, recibiría la Medalla Fields en 1966, aunque no fue este tu único premio; en 1964 ya había ganado el Premio Bôcher por sus contribuciones para resolver la conjetura de Littlewood. Cohen pasó prácticamente toda su carrera en Stanford, enseñando, investigando, y diseñando la técnica "forcing", cuyas aplicaciones no solo se encuentran en los resultados de Paul, sino también en los de muchos otros matemáticos contemporáneos suyos.

UNA MIRADA A LA HISTORIA - Farhud es una palabra en árabe que significa “expropiar, desposeer por la fuerza”, aunque lo que sucedió el...

HABLEMOS DE LA BIBLIA, CON IRIT GREEN - Señor, mi protector, a ti clamo. ¡No te niegues a responderme! Pues si te niegas a...
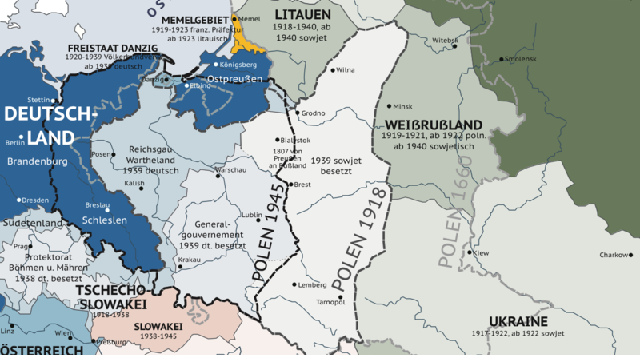
LAS EDADES DEL TOTALITARISMO, CON RICARDO LÓPEZ GÖTTIG - Los territorios polacos anexionados por la Alemania nazi incluyen casi una cuarta parte de las...